Skip to main content

PCA with rotation (Factor Analysis)

Three analyses are presented.

  1. Factor analysis extracting 12 components with a rotated solution.
  2. Factor analysis extracting 4 components (eigen values >1) with a rotated solution.
  3. Factor analysis extracting 5 components with a rotated solution.

An unrotated Factor Analysis of 12 factors is not presented because the results are identical to the previous PCA (except that the loadings are rescaled coefficients).

Analysis 1: Factor analysis extracting 12 components with a rotated solution

NOTE: Although they are present in the output, coefficients and loadings are not shown for factors 6 - 12 because they are not used in the interpretation and their exclusion (from the output) shortens the text.

Principal Component Factor Analysis of the Correlation Matrix

Unrotated Factor Loadings and Communalities

Variable

Factor1

Factor2

Factor3

Factor4

Factor5

Communality

MaxAlt

0.8780

0.0780

-0.1950

-0.3720

-0.104

1.0

MeanAlt

0.7690

-0.1620

0.0250

-0.4990

-0.144

1.0

SDAlt

0.8290

0.2750

-0.3550

-0.0960

0.040

1.0

MeanSlope

0.7710

0.2900

-0.3720

-0.0430

0.255

1.0

Mire

-0.5060

-0.2280

0.1530

-0.5950

-0.247

1.0

Heathland

0.7040

-0.1170

0.0950

0.3530

-0.033

1.0

WetHeath

-0.2280

0.4600

-0.1280

0.0280

-0.743

1.0

Deer

0.7030

0.1030

0.2490

0.2630

-0.317

1.0

Sheep

-0.4610

-0.5420

-0.5780

-0.1610

0.050

1.0

Cattle

0.2130

-0.9140

-0.1040

0.1160

-0.119

1.0

NPP

-0.4230

0.1420

-0.6850

0.2870

-0.199

1.0

Grazed

0.5210

-0.7520

0.0090

0.2260

-0.214

1.0
             

Variance

4.6505

2.1944

1.2284

1.1201

0.915

  

% Var

0.3880

0.1830

0.1020

0.0930

0.076

  


Rotated Factor Loadings and Communalities

Varimax Rotation

Variable

Factor1

Factor2

Factor3

Factor4

Factor5

MaxAlt

0.6740

-0.1110

-0.6480

0.1220

0.0530

MeanAlt

0.3400

-0.1990

-0.8640

0.2190

-0.0400

SDAlt

0.8880

-0.0210

-0.2460

0.0100

0.1650

MeanSlope

0.8930

0.0300

-0.1570

0.0320

0.2500

Mire

-0.2780

0.0540

-0.0180

-0.0180

-0.9380

Heathland

0.2560

-0.2070

-0.1220

0.0880

0.1480

WetHeath

-0.0400

0.1660

0.0430

-0.1010

-0.0060

Deer

0.2140

-0.1150

-0.2070

0.0340

0.1160

Sheep

-0.1540

-0.2100

0.0610

-0.2450

-0.1550

Cattle

-0.0390

-0.9480

-0.0530

0.0790

-0.0140

NPP

-0.0430

0.1100

0.1830

-0.9480

-0.0170

Grazed

0.0770

-0.9200

-0.1750

0.0580

0.0850
           

Variance

2.3801

1.9408

1.3825

1.0519

1.0402

%Var

0.1980

0.1620

0.1150

0.0880

0.0870


1
Interpeting the structure

Select the missing words from the Word Bank.

Because this is Factor Analysis, rather than a , the output includes . These are all 1.0 because all 12 factors have been extracted, meaning that all of the is included in the analyses. The rotation has produced a set of factor loadings that are to either 0 or 1. This simplifies the interpretation. This rotation of the factors has not altered the original data, only our of it. The rotated Factor 1, which accounts for almost of the variation, is mainly composed of the variables. Note that the unrotated Factor 1 accounts for almost 39% of the variation. The rotated Factor is almost entirely Cattle and Grazed, while Factor is concerned with . In Factor 2 the largest loadings are ,this means that a case with a large score on Factor 2 will tend to have values for the amount of grazed vegetation.

Well done, you appear to have a good understanding of the interpretation of this analysis.Important points: (1) Factor Analysis is similar to a PCA, but only common (shared) variation is partitioned. (2) Loadings are correlation coefficients, this means that small values (+ or -) indicate little relationship between a variable and the factor. (3) A negative loading (correlation) means that larger scores for the component are associated with smaller values for the variable.

Word bank: 2, 20%, 3, PCA, Varimax, altitude, closer, communalities, negative, small, topographic, variation, view

Check your answer

Loading Plot

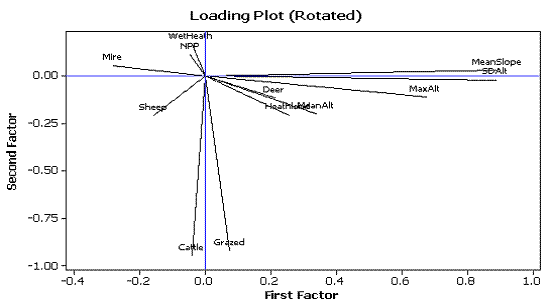Loading plot for factors 1 (x axis) and 2 (y axis).[D]

Factor Score Coefficients: These have been deleted from the output.

Analysis 2: Factor analysis extracting 4 components (eigen values >1) with a rotated solution.

Principal Component Factor Analysis of the Correlation Matrix

Unrotated Factor Loadings and Communalities

Variable

Factor1

Factor2

Factor3

Factor4

Communality

MaxAlt

0.8780

0.0780

-0.1950

-0.3720

0.954

MeanAlt

0.7690

-0.1620

0.0250

-0.4990

0.868

SDAlt

0.8290

0.2750

-0.3550

-0.0960

0.898

MeanSlope

0.7710

0.2900

-0.3720

-0.0430

0.819

Mire

-0.5060

-0.2280

0.1530

-0.5950

0.687

Heathland

0.7040

-0.1170

0.0950

0.3530

0.643

WetHeath

-0.2280

0.4600

-0.1280

0.0280

0.281

Deer

0.7030

0.1030

0.2490

0.2630

0.636

Sheep

-0.4610

-0.5420

-0.5780

-0.1610

0.866

Cattle

0.2130

-0.9140

-0.1040

0.1160

0.905

NPP

-0.4230

0.1420

-0.6850

0.2870

0.751

Grazed

0.5210

-0.7520

0.0090

0.2260

0.887
           

Variance

4.6505

2.1944

1.2284

1.1201

9.193

% Var

0.3880

0.1830

0.1020

0.0930

0.766


Rotated Factor Loadings and Communalities

Varimax Rotation

Variable

Factor1

Factor2

Factor3

Factor4

MaxAlt

0.929

-0.1360

0.1560

0.2180

MeanAlt

0.775

-0.3200

-0.0510

0.4030

SDAlt

0.860

0.0350

0.3960

-0.0080

MeanSlope

0.801

0.0600

0.4130

-0.0570

Mire

-0.189

-0.0090

-0.7960

0.1280

Heathland

0.289

-0.3490

0.6280

0.2080

WetHeath

-0.050

0.4990

0.0110

-0.1700

Deer

0.303

-0.1280

0.6160

0.3840

Sheep

-0.106

-0.3710

-0.5330

-0.6570

Cattle

-0.008

-0.9440

-0.0250

-0.1120

NPP

-0.136

0.2210

0.0150

-0.8270

Grazed

0.145

-0.8880

0.2700

0.0680
         

Variance

3.110

2.3799

2.1217

1.5818

% Var

0.259

0.1980

0.1770

0.1320


Loading Plot

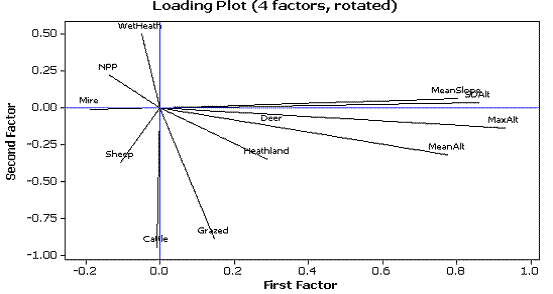Loading plot for factors 1 (x axis) and 2 (y axis).[D]

2
Interpreting the loadings

Decide which statements are valid.

a) All of the variables share a lot of common variability.
b) Almost 3/4 of the variability is retained by the 4 factors.
c) Factor 1 is a measure of the topography and cases with a high score on this factor will tend to behigh with large slopes. They will also have more deer.
d) The second factor is concerned with grazing, mainly cattle and, to a lesser extent, sheep. Cases with a large positive score on this factor will tend to have moreof these large grazers.
e) Sheep are not very highly loaded onto any factor.
f) Factor 4 is related to sheep grazing. Cases with a large negative score have more sheep at lower altitudes, with more NPP.
a) Correcta) No, most communalities are quite large but wetheath has a small communality, with only 28% of its variation shared in common.b) Correctb) 76.6% of variation is retained (sum the % Var and multiply by 100).c) Correctc) The 4 topographic loadings are large and positive. Deer has smaller positive loading. Therefore, cases with a high score on this factor will be as described.d) Correctd) No, the loadings are negative. Therefore, larger factor scores are associated with smaller values for grazing, cattle and sheep.e) Correcte) The loadings would suggest that sheep are associated with factors 2, 3, & 4, but none of the loadings are very large.f) Correctf) The MeanAlt loading is positive, therefore large negative loadings are at lower altitudes. The Sheep and NPP loadings are negative meaning larger values of these are associated with larger negative factor scores.
Check your answer

Factor Score Coefficients: Not shown

Analysis 3: Factor analysis extracting 5 components with a rotated solution.

Principal Component Factor Analysis of the Correlation Matrix

Unrotated Factor Loadings and Communalities

Variable

Factor1

Factor2

Factor3

Factor4

Factor5

Communality

MaxAlt

0.8780

0.0780

-0.1950

-0.3720

-0.104

0.9640

MeanAlt

0.7690

-0.1620

0.0250

-0.4990

-0.144

0.8890

SDAlt

0.8290

0.2750

-0.3550

-0.0960

0.040

0.8990

MeanSlope

0.7710

0.2900

-0.3720

-0.0430

0.255

0.8840

Mire

-0.5060

-0.2280

0.1530

-0.5950

-0.247

0.7470

Heathland

0.7040

-0.1170

0.0950

0.3530

-0.033

0.6440

WetHeath

-0.2280

0.4600

-0.1280

0.0280

-0.743

0.8330

Deer

0.7030

0.1030

0.2490

0.2630

-0.317

0.7360

Sheep

-0.4610

-0.5420

-0.5780

-0.1610

0.050

0.8680

Cattle

0.2130

-0.9140

-0.1040

0.1160

-0.119

0.9190

NPP

-0.4230

0.1420

-0.6850

0.2870

-0.199

0.7910

Grazed

0.5210

-0.7520

0.0090

0.2260

-0.214

0.9330
             

Variance

4.6505

2.1944

1.2284

1.1201

0.915

10.1084

% Var

0.3880

0.1830

0.1020

0.0930

0.076

0.8420


Rotated Factor Loadings and Communalities

Varimax Rotation

Variable

Factor1

Factor2

Factor3

Factor4

Factor5

MaxAlt

0.9420

-0.1530

0.2110

0.0950

-0.0140

MeanAlt

0.8070

-0.3100

0.3230

-0.1730

0.0830

SDAlt

0.8480

0.0150

0.0660

0.4180

-0.0310

MeanSlope

0.7780

0.1050

-0.0010

0.4980

0.1410

Mire

-0.1580

0.0100

-0.0790

-0.8440

-0.0670

Heathland

0.2950

-0.4030

0.3550

0.5170

0.0380

WetHeath

-0.0410

0.2160

-0.0160

-0.1050

-0.8800

Deer

0.3260

-0.2830

0.5700

0.4000

-0.2540

Sheep

-0.1290

-0.2860

-0.8040

-0.3310

0.1180

Cattle

0.0060

-0.9230

-0.1540

-0.0680

0.1980

NPP

-0.1780

0.1120

-0.7220

0.1900

-0.4340

Grazed

0.1660

-0.9300

0.1140

0.1450

0.0870
           

Variance

3.1584

2.2293

1.8167

1.7826

1.1215

%Var

0.2630

0.1860

0.1510

0.1490

0.0930


Loading Plot

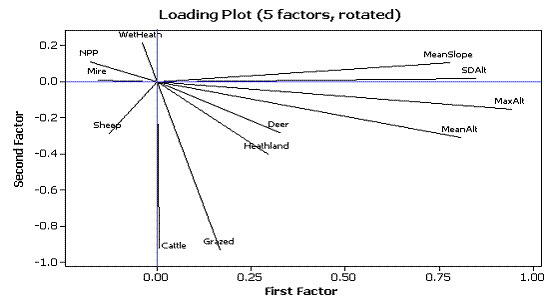Loading plot for factors 1 (x axis) and 2 (y axis).[D]

3
Factor Names

Match the potential factor names to the factor numbers.

a) Wet Heathland
b) Cattle grazing
c) Mires
d) Sheep grazing
e) Topography
The names are based on the patterns of loadings. For example, the two largest loadings on Factor 4 are Mire and MeanSlope. The loadings have different signs, as slope increases the amount of mire decreases. This is reasonable since mires require waterlogged ground which is more likely if the land is flat.
Check your answer

Factor Score Coefficients: Not shown