Distance and similarity measures
Background
Although there are important differences between distances and similarities the two sets of measures are both referred to as distances in these notes. A small distance is equivalent to a large similarity.
There is more than one way to measure a distance. There are distances that are euclidean (can be measured with a 'ruler') and there are other distances, often based on similarity, that are non-Eucliean. For example, in terms of road distance (a euclidean distance) York is closer to Manchester than it is Canterbury. However, if distance (similarity) is measured in terms of a city's characteristics then York is closer to Canterbury.
Distance measures
Three general classes of distance measures can be recognised.
Euclidean metrics
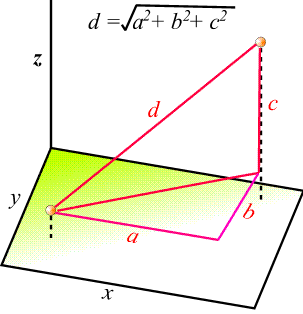
These measure true straight line distances in Euclidean space.
In a univariate example the euclidean distance between two values is the arithmetic difference, i.e. value1 - value2. In the bivariate case the minimum distance is the hypotenuse of a triangle formed from the points. For three variables the hypotenuse will be extended through 3-dimensional space. Although difficult to visualise, an extension of the Pythagoras theorem will give the distance between two points in n-dimensional space.
Note that the distance from Manchester to Chicago would not be Euclidean unless you bored a tunnel through the earth. The flight path of plane would follow the earth's curvature and hence would not be a straight line distance.
Non-Euclidean metrics
Distances that are not straight-line, but which obey certain rules. Let dij is the distance between two cases, i & j.
- dij must be 0 or positive
- dij = dji : e.g. the distance from A to B is the same as that from B to A.
- djj = 0 : a object is identical to itself!
- dik < = dij + djk : when considering three objects the distance between any two of them can not exeed the sum of the distances between the other two pairs. In other words the distances can be constructed as a triangle. For example, if dik = 10 and dij = 3 and djk = 4 it is impossible to construct a triangle, hence the distance measure would not be a non-Euclidean metric.
The Manhattan or City Block metric is an example of this type.
Semi-metrics
Distance measures that obey the first three rules but may not obey the 'triangle' rule. The Cosine measure is an example of this type.
Importance of data types
You also need to take account of the type of data since each has its own set of distance measures. In general there are 3 broad classes:
It is not generally possible, or advisable, to mix data types in a cluster analysis.
Euclidean distances for interval variables
Several distance measures are available in most statistical packages. The following are the most common.
SEUCLID
squared euclidean distance. For any pair of cases the measure is Distance(x,y) = Sum(x - y)2
Therefore SEUCLID is the sum of the squared differences between scores for two cases on all variables, i.e. the squared length of the hypotenuse.
EUCLID
square root of SEUCLID. Note that for two variables this is the normal Pythagoras theorem.
CHEBYCHEV
This is a distance measure. In this the absolute maximum difference between variable scores is used: Distance(x,y) = MAX |x-y|
BLOCK
City Block or Manhattan distance. So named because in most American cities it is not possible to go directly between 2 points. A route which follows the regular grid of roads is used.

Data Transformations
One problem with euclidean distances is that they can be greatly influenced by variables that have the largest values. Consider the following pair of points (200,0.2 and 800,1.0).
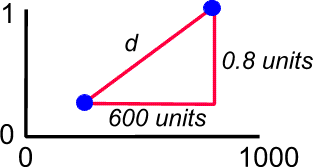
The euclidean distance between them is the square root of (6002 + 0.82), which is the square root of (360000 + 0.64) = 600.0007. Obviously this distance is almost entirely dominated by the variable on the x axis.
One way around this problem is to standardise the variables. For example, if both are forced to have a scale within the range 0 - 1 the two distances become 0.6 and 0.8, which are much more equitable. The value of d is then 1.0, and both variables have contributed significantly to this distance.
Non-euclidean distances for interval data
COSINE - Cosine of vectors of variables. This is a pattern similarity measure. The cosine of the angle between 2 vectors is identical to their correlation coefficient.
| Similarity(x,y) = | Sum (xy) |
| (Sum x2)(Sum y2) |
Count Data
Chi-square measure.
This measure is based on the chi-square test of equality for two sets of frequencies.
Phi-square measure.
This measure is equal to the chi-square measure normalized by the square root of the combined frequency.
Binary Data
There are a surprisingly large number of dissimilarity measures available for binary data, for example SPSS v8.0 lists 27 different ones. All of these binary-based measures use two or more of the values obtained from a simple 2 x 2 matrix of agreement. Note that n = a + b + c + d.
| + | - | |
|---|---|---|
| + | a | b |
| - | c | d |
Many of these measures differ with respect to the inclusion of double negatives (d). Is it valid to say that the shared absence of a character is indicative of similarity? The answer is that it depends on the context, sometimes it is and sometimes it isn't. In particular it depends on the attribute represented by a binary variable. In some cases, e.g. presence or absence of a character, the 0 has an obvious meaning, but in others, such as gender where 0 = male and 1 = female, the meaning of the 0 is less obvious. Nine example measures are listed below. If the measure uses a or d it is a similarity measure, if it uses only b or c it is a measure of dissimilarity.
|
Name
|
Equation
|
Comments
|
|---|---|---|
| Euclidean distance. | SQRT(b+c) | The square root of the sum of discordant cases, minimum value is 0, and it has no upper limit. |
| Squared Euclidean distance | b+c. | The sum of discordant cases, minimum value is 0, and it has no upper limit. |
| Pattern difference | bc/(n**2) | Dissimilarity measure for binary data that ranges from 0 to 1. |
| Variance. | (b+c)/4n | Ranges from 0 to 1 |
| Simple matching | (a+d)/n | This is the ratio of matches to the total number of values. Equal weight is given to matches and nonmatches. |
| Dice. | 2a/(2a + b + c) | This is an index in which joint absences are excluded from consideration, and matches are weighted double. Also known as the Czekanowski or Sorensen measure. |
| Lance and Williams | (b+c)/(2a+b+c) | Range of 0 to 1. (Also known as the Bray-Curtis nonmetric coefficient.) |
| Nei & Lei's genetic distance | 2a/[(a+b)+(a+c)] | |
| Yule coefficient | (ad-bc)/(ad+bc) | This index is a function of the cross-ratio for a 2 x 2 table and is independent of the marginal totals. It has a range of -1 to 1. Also known as the coefficient of colligation. |
Other measures
Measuring the similarity amino acid sequences (text sequences) is difficult and special purpose measures are needed to cope with the consequences of gaps within one or both sequences. One of the most common measures uses the BLAST algorithm (Basic Local Alignment Search Tool, ). BLAST uses a heuristic algorithm to look for local, rather than global, alignments. This enables it to detect relationships among sequences that share only isolated regions of similarity.
Next: joining groups together.
Return to Cluster Analysis.

