Clusters: Clustering Algorithms
Background
Having decided how to measure similarity (the distance measure) we must now choose the clustering algorithm, i.e. the rules which govern how distances are measured between clusters. There are many methods available, the criteria used differ and hence different classifications may be obtained for the same data, even using the same distance measure.This is important since it tells us that, although cluster analysis may provide an objective method for the clustering of cases, there can be subjectivity in the choice of method.
Five clustering algorithms are described.
Average linkage clustering
The dissimilarity between clusters is calculated using average values. Unfortunately, there are many ways of calculating an average. The most common (and recommended if there is no reason for using other methods) is UPGMA - Unweighted Pair-Groups Method Average. The average distance is calculated from the distance between each point in a cluster and all other points in another cluster. The two clusters with the lowest average distance are joined together to form the new cluster.
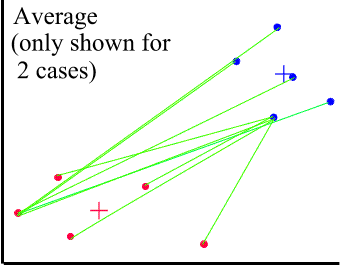
The + signs mark the centres of the two clusters.
There are other methods based on CENTROID and MEDIAN averages. Centroid, or UPGMC (Unweighted Pair-Groups Method Centroid), uses the group centroid as the average. The centroid is defined as the centre of a cloud of points. A problem with the centroid method is that some switching and reversal may take place, for example as the agglomeration proceeds some cases may need to be switched from their original clusters. This makes interpretation of the dendrogram quite difficult.
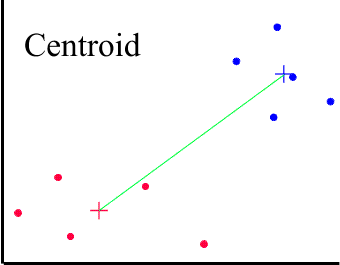
The + signs mark the centres of the two clusters.
COMPLETE LINKAGE CLUSTERING (Maximum or Furthest-Neighbour Method)
The dissimilarity between 2 groups is equal to the greatest dissimilarity between a member of cluster i and a member of cluster j. This method tends to produce very tight clusters of similar cases.
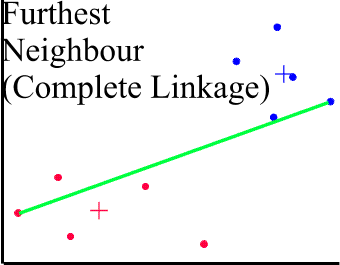
SINGLE LINKAGE CLUSTERING (Minimum or Nearest-Neighbour Method)
The dissimilarity between 2 clusters is the minimum dissimilarity between members of the two clusters. This methods produces long chains which form loose, straggly clusters. This method has been widely used in numerical taxonomy.

WITHIN GROUPS CLUSTERING
This is similar to UPGMA except that clusters are fused so that within cluster variance is minimised. This tends to produce tighter clusters than the UPGMA method.
Ward's method
Cluster membership is assessed by calculating the total sum of squared deviations from the mean of a cluster. The criterion for fusion is that it should produce the smallest possible increase in the error sum of squares.
Which distance measures are compatible with the above algorithms?
Lance and Williams (1967) investigated this question and came to the following conclusions. It appears that most combinations are compatible. The general distance definitions are given in the distance section.
| Algorithm | Euclidean metric | Non-Euclidean metric | Semi-metric |
|---|---|---|---|
| Single |
|
|
|
| Complete |
|
|
|
| Average |
|
|
|
| Median |
|
|
|
| Centroid |
|
|
|
| Ward's |
|
|
|
Lance, G. N. and Williams, W. T. 1967. A general theory of classificatory sorting strategies. Computer Journal, 9: 373-380.
next topic: dendrograms
Short SAQ
1 |

