Skip to main content

Exploratory Data Analyses

There are 252 cases and no missing values.

Descriptive statistics

Variable

Mean

SE

Minimum

Maximum

MaxAlt

677.7

16.4

102.0

1265.0

MeanAlt

331.5

10.7

14.0

895.4

SDAlt

131.4

3.34

13.6

255.7

MeanSlope

13.6

0.286

2.92

26.97

Mire

2.36

0.038

0.041

3.36

Heathland

2.69

0.038

0.41

3.41

WetHeath

1.51

0.041

0.04

2.84

Deer

1.56

0.030

0.04

2.26

Sheep

3.07

0.015

2.59

3.65

Cattle

1.60

0.029

0.45

2.86

NPP

6.56

0.007

6.29

6.89

Grazed

5.05

0.022

4.16

5.99


Relationships between variables

In the matrix scatter plot the variable groups are marked in different colours.

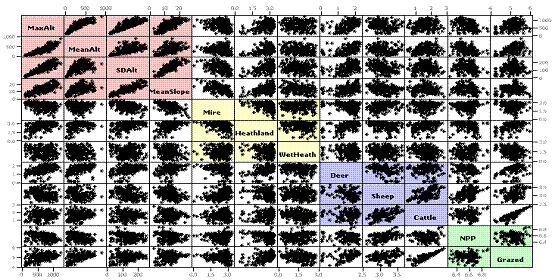Scatter plots for all variable pairs.[D]

Correlation Matrix

Correlation coefficients are significant (p<0.05, uncorrected for multiple testing) if the absolute value is >?????

Variable

Max

Alt

Mean

Alt

SD

Alt

Mean

Slope

Mire

Heath

land

Wet

Heath

Deer

Sheep

Cattle

NPP

MaxAlt

  

0.86

0.84

0.73

-0.27

0.45

-0.08

0.50

-0.28

0.10

-0.30

MeanAlt

0.86

  

0.55

0.47

-0.09

0.38

-0.18

0.46

-0.20

0.23

-0.43

SDAlt

0.84

0.55

  

0.85

-0.45

0.48

-0.04

0.47

-0.33

-0.03

-0.13

MeanSlope

0.73

0.47

0.85

  

-0.51

0.43

-0.14

0.37

-0.30

-0.06

-0.14

Mire

-0.28

-0.09

-0.45

-0.51

  

-0.36

0.03

-0.32

0.33

-0.01

0.08

Heathland

0.45

0.38

0.48

0.43

-0.36

  

-0.21

0.57

-0.30

0.22

-0.24

WetHeath

-0.08

-0.18

-0.04

-0.14

0.03

-0.21

  

-0.06

-0.09

-0.29

0.23

Deer

0.50

0.46

0.47

0.37

-0.32

0.57

-0.06

  

-0.52

0.02

-0.19

Sheep

-0.28

-0.20

-0.33

-0.30

0.33

-0.30

-0.09

-0.52

  

0.39

0.40

Cattle

0.10

0.23

-0.03

-0.06

-0.00

0.22

-0.29

0.02

0.39

  

-0.16

NPP

-0.30

-0.43

-0.13

-0.14

0.08

-0.24

0.23

-0.19

0.40

-0.16

  

Grazed

0.33

0.43

0.20

0.14

-0.20

0.45

-0.29

0.39

0.06

0.86

-0.23


1
Correlations

Which group of variables show the greatest internal correlation?

a) Habitat variables
b) Topographic
c) Grazers
d) Vegetation
Yes, this is clearest in the scatter plots.The topogrpahic variables (Altitude and Slope) show the largest internal correlations. This is relatively clear in both the scatter plots and the correlation coefficients.
Check your answer

2
Uncorrelated variables

Which variables are relatively uncorrelated with the other variables?

a) MaxAlt
b) Cattle
c) Wet heath
d) Grazed
e) Heathland
f) NPP
a) Correcta) This highly correlated with the other topographic variables, and has a reasonable correlation with Heathland and Deer.b) Correct, this has little correlation with the other variables.b) This has little correlation with the other variables. Only sheep has a reasonable correlation.c) Correct, this has little correlation with the other variables.c) This has no correlations > 0.30.d) Correctd) This is highy correlated with cattle and has medium correlations with Heathland and, MeanAlt and Deer.e) Correcte) This has 5 correlation coefficients of approximately 0.4 or greater.f) Correctf) This has two reasonable (0.4+) correlations (MeanAlt and Sheep)
Check your answer

3
Preliminary interpretations

One or more of the following statements is correct.

a) There is sufficient redundancy (correlations) within these data to suggest that a PCA can be used to reduce the dimensionality.
b) It is probable that one of the components will be mainly the topographic variables.
c) It seems probable that the effective dimensionality will be approximately 2.
d) The negative correlations will not contribute to the data structure, i.e. they will be ignored when the components are created.
a) Correct, there are quite a few quite large correlations.a) There are quite a few quite large correlations, suggesting that the effective dimensionality is less than 12.b) Correct, they have a high degree of internal correlation.b) They have a high degree of internal correlation and should be expected to contribute to the same component. Theymay also contribute, differently, to other components.c) Correct, the data structure is too complex to make that assumption.c) No, the data structure is too complex to make that assumption. The correlations do not fall into 2 obvious groups.d) Correct, it is the magnitude of a correlation that matters. not its sign.d) No, it is the magnitude of a correlation that matters. not its sign.
Check your answer