Outline of matrix methods
Background
- Matrix or linear algebra methods make use of data stored as vectors or matrices.
- A vector is either a row or a column of numbers, e.g. the vector [ 12, 34, 24 ] contains three numbers, these could be the x, y ,z coordinates for a point in 3D space.
A matrix is a table of numbers, (see below). These could be the x, y and z coordinates of four points.
|
12 13 17 15 25 26 29 33 18 32 14 28 |
Most normal arithmetic operations are possible on vectors and matrices, e.g. addition, subtraction, multiplication etc, A different set of rules are applied to some of these operations compared with normal arithmetic, although addition and subtraction are easy.
For example, let matrices A and B be
| 4 | 3 | and | 5 | 2 | |||
| 2 | 1 | 4 | 8 |
Then if C = A + B, the contents of C are
| 9 |
5
|
| 6 |
9
|
Subtraction works in a similar way. Note that matrices must have an identical structure (same number of rows and columns) for this to be possible. Multiplication is slightly more complicated, details are not given here except to say that multiplication can only occur when the number of rows in one matrix match the number of columns in the other, and vice-versa.
The following demonstrates the power of matrix algebra methods to deal with potentially difficult problems. Consider the following pair of simultaneous equations.
3x + 4y = 18
2x + 3y = 13
How can we find the values for the two unknowns? The first step is to rewrite the equation in matrix format.
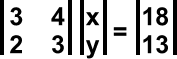
Let A be the matrix
| 3 | 4 |
| 2 | 3 |
x and h are vectors.
| x | = | x | h | = | 18 | |
| y | 13 |
The equation can now be written as A x = h, where x is a vector of our unknown values.
In the same way that any number multiplied by its inverse is 1 (eg 1/4 x 4 = 1), any matrix multiplied by its inverse results in the matrix equivalent of 1, the Unit Matrix, I ( All zeros except the diagonal which is all ones).
If we multiply both sides by the inverse of A we get
A-1 A x = A-1 h
but A-1 A = I therefore
I x = A-1 h
or (we can ignore multiplying by 1)
x = A-1 h
Therefore, if we can find A-1 we can easily solve the equation to obtain the vector x, and hence the values of x and y (x is the product of A-1 and h). There are standard computational methods for finding the inverse of matrix, note that it is not always easy!
For completeness A-1 is
| x | = | 3 | -4 | 18 | = | ( 54 - 52) | = | 2 | |
| y | -2 | 3 | 13 | (-36 + 39) | 3 |
The example above demonstrates how matrix algebra can be a very useful tool, in fact it is essential to multivariate statistics.
Eigen analysis is one matrix method that is essential for many multivariate techniques. It has no counterpart in normal mathematics.
An outline of the mathematical background to PCA is also available, but it is not essential to the unit.

