How Trees are Built and Pruned

Example analysis

The process of building a decision tree is illustrated using a simple data set.

The data are the sex (M,F) of 30 adults. Data are available for the height (cm), weight (kg) and age (years). The aim is to build a tree that predicts the sex of a person from three predictors (height, weight and age).

sex	height	weight	age
F	170	65	43
F	168	62	46
F	163	57	19
F	165	59	52
F	175	69	49
F	173	64	35
F	157	46	33
F	168	60	21
F	170	53	20
F	173	59	21
F	165	51	26
F	160	56	32
F	183	60	48
F	175	58	37
F	165	60	22
M	180	77	54
M	183	75	56
M	183	75	51
M	173	74	26
M	183	78	58
M	168	61	35
M	180	86	42
M	188	81	38
M	173	69	36
M	175	77	27
M	178	79	34
M	185	75	23
M	180	77	54
M	173	79	38
M	170	78	29

The analysis was completed using CTREE (http://www.geocities.com/adotsaha/CTree/CtreeinExcel.html). This is a free, simple decision tree that runs in Excel.

Stage 1

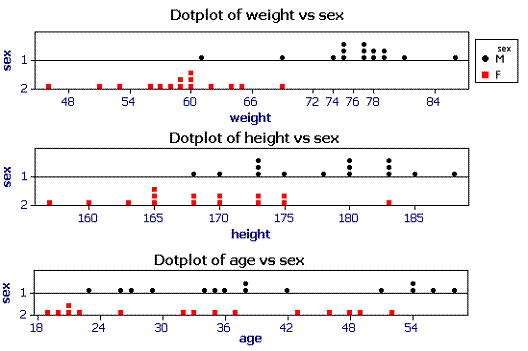
The root node contains all 30 case, 15 males and 15 females. The starting point is finding which variable is the best predictor on a simple binary split. A simple, but repetitive, method is used to find the combination of predictor and split point. In the case of continuous variables (such as these) all possible values for each predictor are tested, e.g. split the cases at weight = 46, 47, 48 ....., height = 151, 152, 153. 154 ..., etc, and find out which of these produces the 'cleanest' split. The aim is to split the data into two groups, ideally one with just males and the other with just females.

1

Finding the first split Which variable split point gives the best split between the sexes? The dot plots below help to visualize the mechanism. a) weight b) height c) age It is clear from the dot plots that weight is the best predictor with a split point somewhere between 70 & 74 kg. The software selects 74. All cases with a weight less than 74 kg are placed in one child node while all cases with a weight greater than 74 kg are placed in the other.

Node 2 is all males (see question feedback) so will not be split further. Node 1 has all of the females and 2 males. In this artificial example node 1 will be split again.

The following dotplots show the Node 1 cases only.

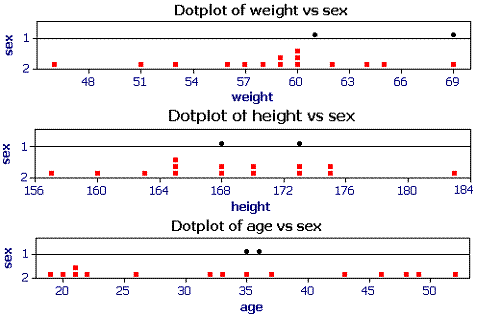
It is less clear how the sexes can be split. The two males are in the middle of the height and age distributions. A split on weight would produce a node with both males and females. The software chooses a split at a weight of 61 kg. Note that this is the same variable used to split the parent node. It is quite normal to use the same variable, with different split points, for different nodes.

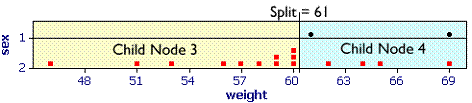
Child node 3 is all females so will not be considered again.

2

Composition of Node 4 Which of the following describes the composition of Node 4? a) All males b) 2 males and 4 females c) 4 males and 2 females d) All females Node 4 has two males (two black circles) and four females (4 red squares). The next dotplots show the distributions for these six cases in node 4.Node 4 has two males (two blck circles) and four females (4 red squares). The next dotplots show the distributions for these six cases in node 4.

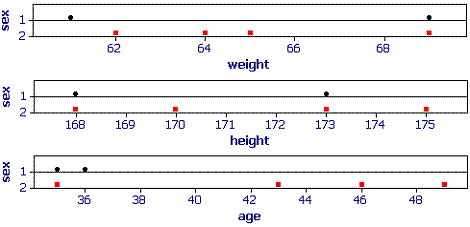
The best split is for age. The software chooses age = 37 years as the split point. This will create two mode child nodes, node 5 has two males and one female plus node 6 with three females.

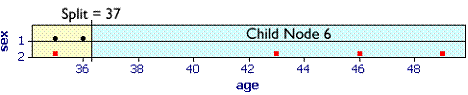
Although node 5 is a mix of two males and one female no further splits are attempted because a stopping rule has been reached (minimum node size to split).

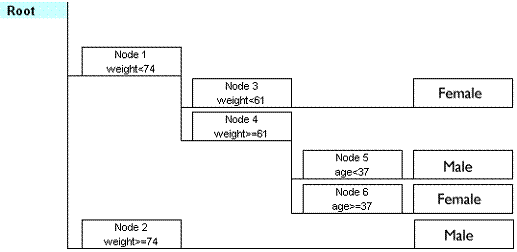
The following shows the decision tree represented by the above decisions. Note that this is slightly modified from the CTREE output.

3	Using the tree What sex does this tree predict for a person aged 25 years and weighing 72 kg? a) Male b) Female CorrectThe answer is male, see the path through the tree in the diagram below.

Using a split with a categorical predictor

If one or more predictors is categorical it is slightly more complex because every combination of predictor and response categories has to be evaluated. The number of potential splits is 2^(k-1)-1 where k is the number of categories of the predictor variable. The fact that a power function is involved means that the number of potential splits increases very rapidly as the number of categories increases, as shown below. The number of splits is low when there are few categories but beyond eight categories the number of splits starts to become quite large.

Categories	Splits
2	1
3	3
4	7
5	15
8	255
16	32767
32	2147483647

4

Calculating categorical splits How many splits must be evaluated if you have recorded behavioural categories as locomotion, sleeping, climbing, grooming, drinking and eating? a) 6 b) 32 c) 31 d) 63 CorrectThe answer is 31. There are 6 behavioural categories so k = 6. 2 to the power 5 is 32. 32 -1 = 31.

Stage 2, pruning the tree, is covered in the next section

Built with courseGenie