Background
This is a 'constrained ordination' technique that is an extension of the original correspondence analysis technique (CA). CCA differs from CA in that rather than looking for implicit relationships between our ordination of, for example, a species matrix and some environmental variables, we look for some explicit relationships. It is, therefore, a direct gradient analysis method.
The reciprocal averaging algorithm is used in the calculation but at each cycle the sample scores are regressed on the environmental variables. This constrains the scores to be linear combinations of the environmental variables.
The example analysis uses the classical data set from the Jongman et al. (1995) book. There are 30 species and 10 environmental variables (some continuous, some ordinal). The question is 'are there any gradients in the species data that can be explained by the environmental variables'?
A brief (very!) explanation of the results is given (See Jongman et al. (1995) for an in depth description). There is also a detailed example on the ordination web site.
Example analysis
CANONICAL CORRESPONDENCE ANALYSIS Data file - E:\Stats\MVSP\Dune.mvs DUNE MEADOW SPECIES DATA (M. BATTERINK AND G. WIJFFELS, 1983) Analysing 30 variables x 20 cases Environmental data file - E:\Stats\MVSP\Dune.mve ENVIRONMENTAL DATA IN FULL FORMAT - DUNE MEADOW DATA Analysing 10 variables x 20 cases Tolerance of eigenanalysis set at 1E-9 Scores scaled by species
| Variable | Weighted mean | Weighted SD | Inflation Factor | |
|---|---|---|---|---|
| A1 | 4.685 | 1.861 | 1.781 | |
| Moisture | 2.801 | 1.731 | 1.850 | |
| Manure | 1.902 | 1.363 | 8.303 | |
| Hayfield | 0.339 | 0.473 | 2.849 | |
| Haypasture | 0.415 | 0.493 | 0.000 | *** |
| Pasture | 0.247 | 0.431 | 1.694 | |
| SF | 0.298 | 0.457 | 3.193 | |
| BF | 0.171 | 0.376 | 2.070 | |
| HF | 0.311 | 0.463 | 0.000 | *** |
| NM | 0.220 | 0.415 | 3.661 |
Multicollinearity detected. Variables marked with "***" will be ignored
in analysis
Axis 1 Axis 2 Axis 3 Axis 4
Eigenvalues 0.461 0.298 0.160 0.134
Percentage 21.804 14.092 7.567 6.320
Cum. Percentage 21.804 35.896 43.462 49.783
Cum.Constr.Percentage 37.815 62.254 75.377 86.338
Spec-env. correlations 0.958 0.902 0.855 0.889>
The species - env. correlations tell us how much of the variation in species composition is 'explained' by the environmental variables. The large figure of 0.958 tells us that we can account for most of the variaiton in species composition by taking account of the environmental varaibles. Later we will discover the contribution that each environmental variable makes to this 'explanation'.
CCA variable scores
These are the scores that will be plotted later.
| Species | Axis 1 | Axis 2 | Axis 3 | Axis 4 |
|---|---|---|---|---|
| Achmil | -0.840 | 0.382 | 0.028 | -0.334 |
| Agrsto | 0.770 | -0.500 | -0.114 | -0.080 |
| Airpra | 0.740 | 1.787 | -1.077 | 0.532 |
| Alogen | 0.354 | -0.970 | -0.347 | 0.139 |
| Antodo | -0.386 | 0.778 | -0.041 | 0.226 |
| Belper | -0.712 | 0.169 | -0.258 | -0.718 |
| Brohor | -0.832 | 0.018 | -0.161 | -0.858 |
| Chealb | 0.931 | -1.647 | -0.693 | 0.027 |
| Cirarv | -0.398 | -0.845 | -0.988 | -0.667 |
| Elepal | 1.497 | -0.090 | 0.575 | -0.383 |
| Elyrep | -0.638 | -0.382 | -0.372 | -0.004 |
| Empnig | 1.206 | 1.549 | -1.452 | 0.558 |
| Hyprad | 0.560 | 1.486 | -0.703 | 0.217 |
| Junart | 0.961 | -0.044 | 0.047 | 0.329 |
| Junbuf | 0.207 | -0.804 | -0.124 | 1.106 |
| Leoaut | 0.000 | 0.431 | 0.032 | -0.067 |
| Lolper | -0.624 | -0.042 | -0.065 | -0.281 |
| Plalan | -0.802 | 0.570 | 0.588 | 0.185 |
| Poapra | -0.459 | -0.040 | -0.129 | -0.156 |
| Poatri | -0.264 | -0.532 | -0.130 | -0.034 |
| Potpal | 2.029 | 0.399 | 2.139 | -0.860 |
| Ranfla | 1.374 | 0.071 | 0.117 | -0.158 |
| Rumace | -0.824 | -0.207 | 0.790 | 0.962 |
| Sagpro | 0.299 | -0.432 | -0.447 | 0.288 |
| Salrep | 0.785 | 1.759 | -1.093 | 0.520 |
| Tripra | -1.112 | -0.059 | 1.015 | 0.933 |
| Trirep | -0.023 | 0.110 | 0.301 | -0.125 |
| Viclat | -0.537 | 1.015 | 0.319 | -0.681 |
| Brarut | 0.135 | 0.253 | 0.138 | 0.225 |
| Calcus | 1.657 | 0.451 | 0.386 | -0.254 |
CCA case scores
| Axis 1 | Axis 2 | Axis 3 | Axis 4 | |
|---|---|---|---|---|
| 1 | -1.219 | -0.497 | -0.935 | -1.252 |
| 2 | -0.864 | -0.250 | -0.536 | -1.703 |
| 3 | -0.315 | -1.010 | -0.900 | -0.638 |
| 4 | -0.237 | -0.931 | -1.271 | -1.047 |
| 5 | -1.146 | 0.240 | 0.914 | 0.624 |
| 6 | -1.031 | 0.368 | 1.799 | 1.495 |
| 7 | -1.034 | 0.151 | 0.963 | 0.649 |
| 8 | 0.697 | -0.717 | -0.108 | -0.276 |
| 9 | -0.053 | -1.005 | -0.489 | 1.241 |
| 10 | -0.963 | 0.600 | 0.236 | -1.458 |
| 11 | -0.507 | 0.932 | 0.146 | -0.515 |
| 12 | 0.354 | -1.442 | -0.524 | 1.825 |
| 13 | 0.472 | -1.619 | -0.907 | 0.655 |
| 14 | 2.021 | 0.266 | 2.543 | -1.804 |
| 15 | 1.958 | 0.049 | 2.169 | -0.860 |
| 16 | 1.932 | -0.691 | 0.802 | -0.528 |
| 17 | -0.388 | 2.770 | -1.065 | 0.905 |
| 28 | -0.311 | 1.495 | -0.147 | -0.074 |
| 29 | 0.665 | 2.873 | -2.664 | 1.724 |
| 30 | 2.001 | 1.003 | -0.264 | 0.328 |
Site scores, constrained by env. data
These are the scores that will be plotted later.
| Axis 1 | Axis 2 | Axis 3 | Axis 4 | |
|---|---|---|---|---|
| 1 | -0.886 | -0.433 | -1.277 | -0.233 |
| 2 | -1.043 | 0.105 | -0.228 | -1.649 |
| 3 | -0.391 | -0.859 | -0.948 | -0.697 |
| 4 | -0.398 | -0.845 | -0.988 | -0.667 |
| 5 | -1.192 | -0.074 | 1.290 | 0.069 |
| 6 | -1.193 | -0.224 | 0.984 | 1.562 |
| 7 | -0.829 | 0.371 | 0.815 | 0.223 |
| 8 | 0.845 | -0.680 | 0.287 | -0.236 |
| 9 | -0.157 | -0.250 | -0.178 | 2.101 |
| 10 | -0.770 | 0.447 | -0.686 | -1.215 |
| 11 | -0.532 | 0.671 | 0.982 | -0.913 |
| 12 | 0.545 | -1.314 | -0.112 | 1.362 |
| 13 | 0.931 | -1.647 | -0.693 | 0.027 |
| 14 | 2.199 | 0.792 | 2.109 | -0.791 |
| 15 | 1.858 | 0.006 | 2.169 | -0.930 |
| 16 | 1.398 | -1.131 | 0.007 | -0.411 |
| 17 | 0.040 | 2.145 | -0.515 | 0.492 |
| 28 | -0.315 | 2.272 | -0.003 | 0.317 |
| 29 | 1.206 | 1.549 | -1.452 | 0.558 |
| 30 | 1.192 | 1.577 | -1.532 | 0.619 |
Canonical coefficients
These are the 'regression coefficients' that are used to calculate the scores. We can use these, and the intraset correlations to interpret our axes. Thus, the first axis is primarily related to soil moisture, whilst the second axis is related to manuring.
| Spec. Axis 1 | Spec. Axis 2 | Spec. Axis 3 | Spec. Axis 4 | |
|---|---|---|---|---|
| A1 | 0.124 | -0.265 | 0.746 | -0.566 |
| Moisture | 0.684 | -0.368 | -0.471 | -0.014 |
| Manure | -0.031 | -0.126 | -0.531 | -1.725 |
| Hayfield | -0.062 | 0.206 | -0.235 | -0.419 |
| Haypastu | 0.000 | 0.000 | 0.000 | 0.000 |
| Pasture | 0.210 | 0.204 | 0.354 | -0.228 |
| SF | 0.207 | -0.109 | -0.403 | 0.129 |
| BF | 0.077 | 0.081 | -0.336 | -1.300 |
| HF | 0.000 | 0.000 | 0.000 | 0.000 |
| NM | 0.392 | 0.796 | -0.577 | -1.161 |
We are given information about interset and intraset correlations. This can be a little confusing.
Intraset correlations are the correlations between the environmental variables
and the axis scores (similar to the structure matrix in a discriminant
analysis)
Interset correlations are the correlations between the site scores (derived
from the species scores) and the environmental variables. You can derive the
interset correaltion from the intraset correlations if you multiply the latter
by R, the species-environment correlation. For example, the intraset
correlation between A1 and axis 1 is 0.563. The species-environment correlation
for axis 1 is 0.958. 0.563 x 0.958 is 0.593, the interset correlation between
A1 and axis 1.
Interset correlations between env. variables and site scores
| Envi. Axis 1 | Envi. Axis 2 | Envi. Axis 3 | Envi. Axis 4 | |
|---|---|---|---|---|
| A1 | 0.539 | -0.156 | 0.504 | -0.097 |
| Moisture | 0.883 | -0.153 | -0.120 | 0.151 |
| Manure | -0.296 | -0.690 | -0.169 | -0.160 |
| Hayfield | -0.072 | 0.545 | -0.216 | 0.251 |
| Haypastu | -0.165 | -0.499 | -0.113 | -0.077 |
| Pasture | 0.268 | -0.028 | 0.366 | -0.187 |
| SF | 0.142 | -0.627 | -0.360 | -0.077 |
| BF | -0.349 | 0.158 | -0.025 | -0.519 |
| HF | -0.346 | -0.105 | 0.376 | 0.464 |
| NM | 0.546 | 0.666 | 0.001 | 0.038 |
Intraset correlations between env. variables and constrained site scores
| Envi. Axis 1 | Envi. Axis 2 | Envi. Axis 3 | Envi. Axis 4 | |
|---|---|---|---|---|
| A1 | 0.563 | -0.173 | 0.589 | -0.109 |
| Moisture | 0.922 | -0.170 | -0.140 | 0.170 |
| Manure | -0.309 | -0.765 | -0.197 | -0.180 |
| Hayfield | -0.076 | 0.605 | -0.252 | 0.282 |
| Haypastu | -0.172 | -0.554 | -0.132 | -0.086 |
| Pasture | 0.279 | -0.031 | 0.428 | -0.211 |
| SF | 0.148 | -0.696 | -0.421 | -0.086 |
| BF | -0.364 | 0.175 | -0.030 | -0.584 |
| HF | -0.361 | -0.116 | 0.439 | 0.522 |
| NM | 0.570 | 0.738 | 0.001 | 0.043 |
Biplot scores for env. variables
These are the intraset correlations, they are used to place arrows on the plots (see later). These are equivalent to the loading plots used in PCA.
| Axis 1 | Axis 2 | Axis 3 | Axis 4 | |
|---|---|---|---|---|
| A1 | 0.563 | -0.173 | 0.589 | -0.109 |
| Moisture | 0.922 | -0.170 | -0.140 | 0.170 |
| Manure | -0.309 | -0.765 | -0.197 | -0.180 |
| Hayfield | -0.076 | 0.605 | -0.252 | 0.282 |
| Haypastu | -0.172 | -0.554 | -0.132 | -0.086 |
| Pasture | 0.279 | -0.031 | 0.428 | -0.211 |
| SF | 0.148 | -0.696 | -0.421 | -0.086 |
| BF | -0.364 | 0.175 | -0.030 | -0.584 |
| HF | -0.361 | -0.116 | 0.439 | 0.522 |
| NM | 0.570 | 0.738 | 0.001 | 0.043 |
Centroids of env. variables
| Axis 1 | Axis 2 | Axis 3 | Axis 4 | |
|---|---|---|---|---|
| A1 | 0.224 | -0.069 | 0.234 | -0.043 |
| Moisture | 0.570 | -0.105 | -0.087 | 0.105 |
| Manure | -0.222 | -0.548 | -0.141 | -0.129 |
| Hayfield | -0.106 | 0.845 | -0.353 | 0.394 |
| Haypastu | -0.204 | -0.658 | -0.157 | -0.103 |
| Pasture | 0.488 | -0.055 | 0.748 | -0.369 |
| SF | 0.228 | -1.068 | -0.646 | -0.133 |
| BF | -0.803 | 0.386 | -0.066 | -1.288 |
| HF | -0.538 | -0.173 | 0.654 | 0.778 |
| NM | 1.073 | 1.388 | 0.002 | 0.080 |
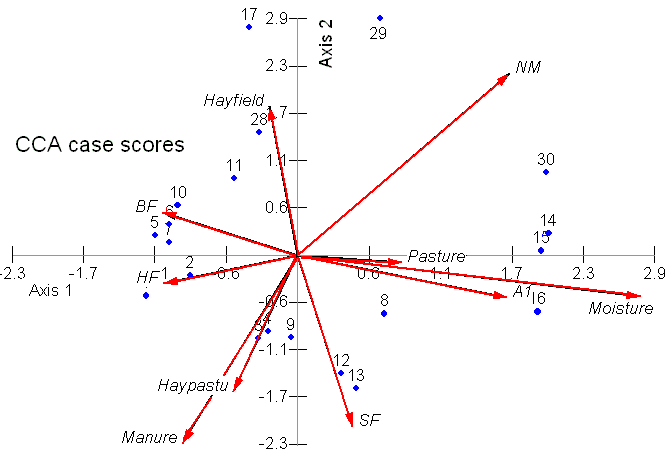
The lengths and positions of the arrows provide information about the relationship between the original environmental variables and the derived axes. Arrows that are parallel to an axis (e.g. moisture and axis 1) indicate a correlation, the length of the arrow tells us about the strength of that correlation. Thus, pasture is related to axis 1 but not as strongly as moisture. Neither of these is related to axis 2.
On the above plot only the site scores are shown, as blue dots. (We could also plot the species scores). Consider site 17, it has a high score of axis 2. What does this mean? Axis 2 is associated with manuring, however because the correlation between manure and axis 2 is negative (also shown the direction of the manure arrow), large positive scores on axis 2 should have low values for manure, whilst large negative values on axis 2 should have lots of manure. Thus we would expect site 17 to have little manuring, whilst site 13 would have lots. Similarly, sites 5 and 16 are at opposite ends of the moistrure gradient.
The second output is from the free plrcacca program. Although the scores differ from those produced by MVSP they are almost perfectly correlated and hence they 'tell the same story'.
Linear ordination and canonical analysis Vladimir Makarenkov - Pierre Legendre, Universite de Montreal Input file: dune.dat 20 objects 30 response variables (matrix Y) 10 explanatory variables (matrix X) Maximum number of canonical eigenvalues = 30 Maximum number of non-canonical eigenvalues = 30 Total inertia (total CA variance) = 2.11526 Mean coefficient of multiple determination R^2 = 0.56612 (CCA) Percentage of the total variance of Q (xi-square of Y) accounted for = 57.98499 Mean squared difference = 0.00148121559 *** Canonical correspondence analysis *** Canonical eigenvalues 0.4646 0.2983 0.1586 0.1372 0.0667 0.0410 0.0325 0.0268 0.0005 % of total variance of CA 21.9658 14.1037 7.4999 6.4882 3.1537 1.9407 1.5398 1.2680 0.0248 Cumulative % of total variance of CA 21.96585 36.06958 43.56954 50.05776 53.21155 55.15226 56.69207 57.96014 57.98495 Cumulative % of canonical variance 37.8819 62.2051 75.1394 86.3289 91.7679 95.1148 97.7703 99.9572 100.000 Sum of all canonical eigenvalues 1.22653 Scaling = 1: sites at centroids of species Species scores (matrice V)
The first two axes have correlations of -0.999 and -0.995 with the CCA variable scores from MVSP
| 1.21565 | -0.78363 | -0.19893 | -0.79069 | 0.43849 | -1.28333 | -0.12902 | 0.13564 | 1.54783 |
| -1.14829 | 0.87988 | 0.27379 | -0.28977 | 0.22047 | 0.62641 | 0.83905 | 0.27188 | -0.40198 |
| -1.05655 | -3.75029 | 2.81111 | 0.97933 | 0.92634 | 1.40561 | 1.29766 | -0.81923 | 3.45419 |
| -0.49720 | 1.65646 | 1.07352 | 0.24680 | -0.81682 | 0.02558 | 0.44513 | 0.21300 | -0.01585 |
| 0.53383 | -1.58228 | 0.18821 | 0.67246 | 1.32327 | -0.46331 | 0.59752 | 2.06375 | 1.11378 |
| 1.03117 | -0.33883 | 0.14021 | -1.95396 | 1.39977 | -0.95132 | 2.15569 | 0.80608 | -1.85766 |
| 1.15929 | -0.05188 | -0.09296 | -2.21447 | 0.90476 | -2.30910 | -0.92637 | 0.73299 | -1.94803 |
| -1.31802 | 2.83783 | 2.26299 | -0.26115 | 0.62653 | -2.58721 | 2.45388 | -1.35340 | 3.49615 |
| 0.49610 | 1.32809 | 1.73922 | -2.32530 | 1.73357 | 4.26325 | 3.20684 | -0.85762 | -5.13821 |
| -2.21725 | 0.25860 | -1.49957 | -0.78658 | 0.36583 | 0.74747 | -0.83948 | 1.16241 | 0.45139 |
| 0.97044 | 0.69800 | 0.91123 | -0.32295 | 1.58675 | 0.41997 | 1.19920 | 0.55620 | 1.47328 |
| -1.79363 | -2.80624 | 3.75530 | 0.69670 | 1.77031 | -0.95151 | -2.69889 | -1.99534 | -2.91277 |
| -0.79251 | -2.95311 | 1.75187 | 0.26687 | -1.61935 | -0.02451 | -0.41158 | -0.74493 | 1.61222 |
| -1.37821 | 0.08261 | 0.09134 | 0.89111 | 1.62026 | -1.26754 | -3.20518 | 0.66986 | 0.44244 |
| -0.27525 | 1.43853 | 0.95938 | 2.99808 | -1.69221 | -1.93412 | 0.72045 | 0.39065 | 1.48854 |
| 0.01179 | -0.78947 | -0.17693 | -0.11584 | -0.26215 | -0.42628 | -0.05183 | -0.73154 | -0.22464 |
| 0.94528 | 0.13211 | 0.01178 | -0.89589 | -0.81375 | 1.26357 | -0.88564 | -0.89847 | 0.60622 |
| 1.16305 | -0.98804 | -1.44401 | 0.81191 | -0.38997 | 1.01399 | 0.33839 | 1.81208 | -0.12225 |
| 0.70690 | 0.06445 | 0.20818 | -0.54250 | -0.19691 | 0.86578 | -0.61789 | -0.15328 | 0.56336 |
| 0.38322 | 0.94328 | 0.39658 | -0.14167 | 0.59440 | -0.33600 | -0.28090 | 0.06489 | -0.02941 |
| -3.03005 | -0.37537 | -5.81484 | -1.21222 | 2.53338 | -1.18835 | 4.94791 | -5.41526 | 3.35132 |
| -2.02387 | -0.08055 | -0.26429 | -0.38995 | 1.05243 | -0.10776 | -1.13099 | -0.72685 | 0.35691 |
| 1.16021 | 0.51560 | -1.39755 | 2.95236 | 0.97938 | 0.27522 | -0.04154 | 0.43887 | -0.79921 |
| -0.41799 | 0.69535 | 1.25801 | 0.60250 | -1.19930 | -0.51082 | 0.14818 | -0.59436 | -0.73879 |
| -1.12004 | -3.15158 | 2.68500 | 0.78511 | 1.08951 | 0.70348 | 0.37957 | -0.90160 | -2.60232 |
| 1.54497 | 0.29594 | -1.97287 | 2.89017 | 1.12479 | 1.95718 | -1.33612 | -2.53525 | -1.84652 |
| 0.00300 | -0.15742 | -0.83743 | -0.12601 | -0.69555 | -1.47527 | -0.17901 | -0.74859 | -0.43475 |
| 0.85737 | -1.76980 | -1.33660 | -1.59870 | -5.85915 | -2.53949 | 0.89542 | 2.72120 | 0.04874 |
| -0.18508 | -0.39085 | -0.28432 | 0.65657 | -0.53802 | 0.05001 | 1.05423 | -0.35396 | -0.58319 |
| -2.54556 | -0.70573 | -1.11287 | -0.58760 | -1.76386 | 1.99832 | -0.14557 | 2.74732 | -1.12204 |
Site scores (matrice F)
| 0.85047 | 0.28208 | 0.28635 | -0.60040 | 0.08280 | 0.66848 | -0.25362 | -0.24512 | 0.77106 |
| 0.58513 | 0.12659 | 0.09142 | -0.63668 | 0.19912 | -0.38781 | -0.04664 | -0.08676 | -0.02568 |
| 0.22589 | 0.53320 | 0.33572 | -0.31849 | -0.02454 | 0.21633 | 0.17846 | -0.07551 | 0.10629 |
| 0.16155 | 0.47912 | 0.41926 | -0.48240 | 0.11736 | 0.21684 | 0.32462 | -0.08335 | -0.39549 |
| 0.76303 | -0.11787 | -0.32591 | 0.30391 | 0.47940 | -0.01830 | 0.11865 | 0.32324 | -0.07011 |
| 0.68332 | -0.15464 | -0.61344 | 0.66777 | 0.07936 | 0.27146 | -0.13999 | -0.17026 | -0.19457 |
| 0.69349 | -0.06145 | -0.33838 | 0.31219 | -0.01913 | 0.07664 | -0.20437 | 0.04683 | 0.01841 |
| -0.46330 | 0.38727 | 0.06273 | -0.11721 | -0.01176 | 0.05900 | -0.45263 | -0.03770 | 0.07438 |
| 0.04889 | 0.54069 | 0.30566 | 0.39603 | 0.09223 | -0.23024 | -0.06804 | 0.05287 | 0.30079 |
| 0.64557 | -0.33381 | -0.21947 | -0.47219 | -0.06725 | -0.41751 | -0.08464 | 0.19443 | 0.00338 |
| 0.36110 | -0.49437 | -0.14389 | -0.18110 | -0.95497 | 0.08885 | -0.09285 | -0.18818 | 0.10045 |
| -0.23423 | 0.75704 | 0.38116 | 0.64492 | -0.50415 | -0.36975 | 0.36461 | -0.05745 | -0.12966 |
| -0.31402 | 0.84210 | 0.47945 | 0.18484 | -0.14198 | -0.34734 | 0.14682 | -0.09340 | 0.14097 |
| -1.40461 | -0.07101 | -1.12047 | -0.45199 | -0.09318 | 0.04968 | 0.24467 | -0.06301 | 0.00284 |
| -1.33198 | 0.03690 | -0.89632 | -0.14584 | 0.49441 | -0.09911 | 0.04832 | -0.30446 | 0.26852 |
| -1.31993 | 0.39838 | -0.29464 | -0.14728 | 0.05798 | 0.36278 | -0.23397 | 0.59292 | -0.09039 |
| 0.26167 | -1.65292 | 0.42982 | 0.29670 | 0.21886 | 0.02557 | 0.25730 | 0.49371 | 1.17021 |
| 0.22276 | -0.77837 | -0.03521 | -0.03802 | -0.33738 | 0.03900 | 0.34978 | -0.09151 | -0.53443 |
| -0.44119 | -1.66293 | 1.08696 | 0.43681 | -0.04489 | -0.14329 | 0.09369 | -0.43078 | 0.09881 |
| -1.36040 | -0.50243 | 0.10562 | 0.06345 | 0.34632 | 0.30583 | -0.35268 | 0.21407 | -0.52151 |
Site scores (matrice Z)/ linear comb. of explanatory var.
The first two axes have correlations of -0.997 and -0.987 with the site scores (constrained by env. data) from MVSP
| 0.78772 | 0.35179 | 0.57119 | -0.31768 | -0.03759 | 0.40864 | 0.16853 | -0.10279 | 0.03124 |
| 0.70857 | -0.08500 | -0.01239 | -0.57622 | -0.01781 | -0.23383 | -0.11018 | -0.25914 | 0.02236 |
| 0.24642 | 0.42746 | 0.27907 | -0.34797 | 0.13190 | 0.18341 | 0.10899 | -0.01854 | 0.02134 |
| 0.23428 | 0.39579 | 0.27689 | -0.32080 | 0.11742 | 0.17515 | 0.09859 | -0.02167 | 0.02011 |
| 0.80152 | 0.09674 | -0.46026 | 0.12651 | 0.43838 | -0.06349 | 0.11487 | 0.32058 | 0.02280 |
| 0.76596 | 0.16261 | -0.24008 | 0.60904 | -0.01088 | 0.02805 | -0.03339 | -0.25505 | 0.02166 |
| 0.53089 | -0.10787 | -0.34358 | 0.12834 | -0.06555 | 0.35552 | -0.25361 | 0.01702 | 0.02131 |
| -0.50186 | 0.30564 | -0.08768 | -0.05616 | 0.22459 | 0.10151 | -0.47324 | 0.01405 | 0.02230 |
| 0.11792 | 0.10934 | 0.19432 | 0.75816 | 0.04485 | -0.23795 | -0.11001 | 0.12480 | 0.02360 |
| 0.48362 | -0.26589 | 0.15500 | -0.45656 | -0.02368 | -0.39851 | -0.02952 | 0.18532 | 0.02219 |
| 0.40741 | -0.33068 | -0.45904 | -0.26849 | -0.75695 | -0.10959 | -0.08395 | 0.01987 | 0.02361 |
| -0.33027 | 0.70334 | 0.20530 | 0.53765 | -0.40588 | -0.11786 | 0.23848 | -0.06870 | 0.02392 |
| -0.60862 | 0.84619 | 0.35999 | -0.03751 | 0.04357 | -0.10607 | 0.07407 | -0.03497 | 0.02464 |
| -1.58806 | -0.34502 | -0.92953 | -0.15475 | -0.13299 | 0.12638 | 0.05337 | 0.00463 | 0.02282 |
| -1.22013 | 0.12021 | -0.91349 | -0.18132 | 0.47454 | -0.22368 | 0.25723 | -0.29247 | 0.02631 |
| -0.98762 | 0.61183 | 0.02419 | -0.17952 | -0.31217 | 0.13894 | -0.00269 | 0.30620 | 0.02238 |
| 0.02657 | -1.54171 | 0.22226 | 0.19092 | -0.02088 | 0.20298 | 0.23166 | 0.02668 | 0.02963 |
| 0.31012 | -1.18637 | -0.08120 | 0.10922 | -0.01881 | 0.20123 | 0.29063 | 0.07222 | 0.02192 |
| -0.82961 | -0.83761 | 0.59673 | 0.09395 | 0.11987 | -0.03893 | -0.09377 | -0.05219 | 0.02128 |
| -0.82490 | -0.85501 | 0.62993 | 0.11148 | 0.10316 | -0.03355 | -0.10381 | -0.06229 | 0.02125 |
Biplot scores of explanatory variables; multiple linear correlations
between the explanatory variables X and the site scores Z
| -0.26628 | 0.14186 | -0.16881 | 0.06005 | 0.04934 | -0.01928 | 0.06065 | -0.04640 | 0.00492 |
| -0.43487 | 0.08712 | 0.12015 | 0.04040 | 0.01820 | -0.03644 | -0.03866 | 0.02102 | 0.00119 |
| 0.22172 | 0.30155 | 0.09256 | -0.10161 | 0.04274 | 0.09264 | -0.04212 | 0.01393 | -0.00203 |
| 0.03567 | -0.23375 | 0.07206 | 0.06409 | 0.05387 | -0.05018 | 0.01190 | 0.05406 | -0.00023 |
| 0.08216 | 0.20558 | 0.04001 | -0.03088 | 0.01275 | 0.00263 | 0.04887 | -0.07611 | 0.00168 |
| -0.13306 | 0.02168 | -0.12484 | -0.03507 | -0.07370 | 0.05208 | -0.06890 | 0.02764 | -0.00167 |
| -0.06679 | 0.25036 | 0.11758 | -0.04846 | -0.02974 | 0.04281 | 0.05211 | 0.00594 | 0.00133 |
| 0.16844 | -0.06811 | -0.02309 | -0.13931 | -0.06987 | -0.08129 | -0.02108 | -0.00650 | -0.00055 |
| 0.16598 | 0.05325 | -0.08807 | 0.15127 | 0.05681 | 0.01491 | -0.06316 | 0.01679 | -0.00232 |
| -0.26457 | -0.27381 | -0.01041 | 0.01101 | 0.03281 | 0.00993 | 0.03217 | -0.01941 | 0.00163 |
Biplot scores of centroids of binary explanatory variables
| 0.07627 | -0.47548 | 0.14743 | 0.12859 | 0.11124 | -0.10185 | 0.01831 | 0.11119 | 0.02276 |
| 0.14577 | 0.35487 | 0.07012 | -0.05504 | 0.02380 | 0.00468 | 0.07855 | -0.13021 | 0.02308 |
| -0.33436 | 0.05467 | -0.31627 | -0.09078 | -0.18553 | 0.13250 | -0.18088 | 0.07157 | 0.02240 |
| -0.14538 | 0.55869 | 0.26357 | -0.10989 | -0.06464 | 0.09575 | 0.11045 | 0.01460 | 0.02309 |
| 0.54353 | -0.21868 | -0.07303 | -0.44807 | -0.22213 | -0.26037 | -0.07336 | -0.01948 | 0.02264 |
| 0.36312 | 0.11488 | -0.18969 | 0.32584 | 0.12476 | 0.03241 | -0.14252 | 0.03769 | 0.02233 |
| -0.71983 | -0.74930 | -0.02749 | 0.02846 | 0.09150 | 0.02728 | 0.08208 | -0.05175 | 0.02323 |
Percentage of variance associated with
matrix Y (not permuted)
Percentage of variance (linear regression) = 57.66018
Permutation tests begin
P(Lin)= 0.00990
Examples
from the literature.
Rottenborn, SC. 1999. Predicting the impacts of urbanization on riparian bird
communities. Biological Conservation, 88: 289-299.
French, BW, Elliott, NC. 1999. Temporal and spatial distribution of ground beetle
(Coleoptera:Carabidae) assemblages in grasslands and adjacent wheat fields.
Pedobiologia, 43: 73-84.
French, BW, Elliott, NC, Berberet, RC. 1998. Reverting conservation reserve
program lands to wheat and livestock production: Effects on ground beetle (Coleoptera:
Carabidae) assemblages. Environmental Entomology, 27: 1323-1335.
Lara, EN, Gonzalez, EA. 1998. The relationship between reef fish community structure
and environmental variables in the southern Mexican Caribbean. Journal of
Fish Biology, 53: 209-221.
Syms, C. 1998. Disturbance and the structure of coral reef fish communities
on the reef slope. Journal of Experimental Marine Biology and Ecology,
230: 151-167.
OliveiraFilho, AT, Curi, N, Vilela, EA, Carvalho, DA. 1998. Effects of canopy
gaps, topography, and soils on the distribution of woody species in a central
Brazilian deciduous dry forest. Biotropica, 30: 362-375.
Lammerts, EJ, Grootjans, AP. 1998. Key environmental variables determining the
occurrence and life span of basiphilous dune slack vegetation. Acta Botanica
Neerlandica, 47: 369-392.
Read, HJ, Martin, MH, Rayner, JMV. 1998. Invertebrates in woodlands polluted
by heavy metals - An evaluation using canonical correspondence analysis. Water
Air and Soil Pollution, 106: 17-42.
Clenaghan, C, Giller, PS, OHalloran, J, Hernan, R. 1998. Stream macroinvertebrate
communities in a conifer-afforested catchment in Ireland: relationships to physico-chemical
and biotic factors. Freshwater Biology, 1998,40: 175-193.
Izhaki, I, Adar, M. 1997. The influence of land use and physico-chemical factors
on the effects of post-fire management on bird community succession. International
Journal of Wildland Fire, 7: 335-342.

Resources
Jongman, R.H.G., ter Braak, C.J.F. and van Tongeren, O.F.R. (eds) 1995. Data analysis in community and landscape ecology. Cambridge University Press. (ter Braak developed the CCA algorithm)
Pierre Legendre's free plrcacca software can be used to carry out a standard CCA (and redundancy analysis) analysis. In addition it is able to carry out an extension to the normal CCA algorithm in that the linear regression model can be replaced by a polynomial regression.
The ordination web site has a detailed list of available software.

