Decision and Regression Trees
Background
Skip to the next section for a more detailed description of decision trees.
Decision and regression trees are an example of a machine learning technique. You can find out more about the machine learning methods, and their use with ecological data, in Fielding, A. H. (1999) (editor) Ecological Applications of Machine Learning Methods, Kluwer Academic. A clue to how they function is provided by their alternative name of recursive partitioning methods.
- As with all regression techniques it is assumed that there is a single response variable and one or more predictor variables.
- If the response variable is categorical classification or decision trees are created (equivalent to discriminant analysis or logistic regression).
- If the response variable is continuous regression trees (equivalent to multiple regression) are produced.
- Predictor variables can be a mixture of continuous and categorical variables.
- The final output is a tree where we decide which branch to follow after applying some test to one or more variables.
In certain circumstances they have an advantage over more common supervised learning methods such as discriminant analysis. In particular, they do not have to conform to the same probability distrubution restrictions. There is also no assumption of a linear model or the need to pre-specify a probability distribution for the errors. They are particularly useful when the predictors may be associated in some non-linear fashion. The advantages of these approaches can be summarised as follows.
- Non-parametric, do not require specification of a functional form (e.g. a general linear model).
- Learn by induction (generalizing from examples) – but this does not guarantee the correct tree.
- Preselection of variables is not needed (a robust stepwise selection method is used).
- Invariant to monotonic predictor transformations, e.g. logarithmic transformations are not needed.
- Same variable can be reused in different parts of a tree, i.e. context dependency automatically recognized.
- Unlike a maximum likelihood method no single dominant data structure (e.g. normality) is assumed or required.
- Robust to the effects of outliers (see below).
- Mixed data types can be used.
- Surrogate variables can be used for missing values.
Decision points are called nodes, and at each node the data are partitioned. Each of these partitions is then partitioned independently of all other partitions, hence the alternative name of recursive partitioning. This could carry on until each partition consisted on one case. This would be a tree with a lot of branches and as many terminal segments (leaves) as there are cases. Normally some 'stopping rule' is applied before arriving at this extreme condition. Inevitably this may mean that some partitions are 'impure' (cases are a mixture of classes), but it is necessary to balance accuracy against generality. A tree which produced a perfect classification of training data would probably perform poorly with new data.
The following diagram summarises the main characteristics of a classification tree for a problem with a binary response (Groups I and II) and four predictors (A, C & D are continuous, B is categorical).
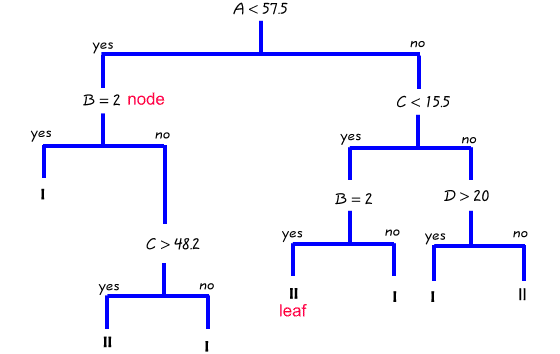
The data are first split (partitioned) into cases with values for A above or below 57.5. The left side of the tree (A<57.5) is next split on the value of B (Y/N). If B = Yes a terminal node is reached in which all cases have B=Yes and A <57.5. If B=No the cases are next split by variable C (above or below C = 48.2). On the right side of the tree (A>57.5) the cases are split depending on the value of C (above or below 15.5). Cases with C<15.5 are split using variable B while those with C>15.5 are split using variable D.
The next section describes decision trees in more detail.
A separate page describes the random Forest algorithm.
Resources
QUEST is Windows-based Public domain CART package. It is available from http://www.stat.wisc.edu/~loh.
There is a nice, free, classification / decision tree addin for Excel available from http://www.geocities.com/adotsaha/CTree/CtreeinExcel.html.
The AI-depot has a short description of recursive partitioning, linked to a discussion list.
Chapter 5 of the book Machine Learning, Neural and Statistical Classification
edited by D. Michie, D.J. Spiegelhalter, C.C. Taylor describes decision trees.
The entire book can be downloaded
as a pdf file (1.79 Mb).
John Bell has written a chapter on the use of decision trees for ecological applications. The reference is: Bell, J. F. (1999) Tree-based methods. The use of classification trees to predict species distributions. In A. Fielding (ed) Machine learning methods for ecological applications. Kluwer Associates.
Self assessment questions
This series of questions uses the CTREE Excel add-in program (see above) and a datafile loosely based on pronghorn antelope data file (PP30-36 in Manly et al (2002) Resource Selection by Animals (2nd Edition), Kluwer Academic). You will need both CTREE and the datafile to fully answer these questions.

