MDS or Principal Coordinate Analysis
Multidimensional Scaling (MDS), which is also known as Principal Coordinates Analysis (PCO), is a more general projection method than PCA. This is because PCO can use any distance matrix. However, because PCO uses a distance matrix all information about the original variables is lost and the analysis relates only to the cases. However, this does mean that it is useful when there are a large number of predictors relative to the number of cases. If the distance matrix uses Euclidean distances a PCO and a PCA analysis would produce identical projections of the cases, albeit with some possible reflections or translations.
The differences between PCO and PCA can be summarised in three points.
- PCA searches for patterns in the variables, PCO searches for similarities between cases.
- PCA reduces variable dimensionality by an eigen analysis of a correlation or covariance matrix. PCO analyses a distance matrix. Many different distance matrices can be used as long as they metric, in particular they must obey the 'triangle' rule.
- The result of a PCO is a set of coordinates on a number of derived axes such that similar cases are close together. It is not possible to associate these axes with any variables.
The classic example of a PCO is an analysis of the types of inter-city distance tables that are common in most road atlases. A table such as this is a distance matrix. If these data are entered into a PCO each city will have coordinates on the derived axes. If you now plot a graph of the coordinates on the first two axes you will notice that a map of, for example, Britain is redrawn (at least in terms of the relative positions of the cities - but note that it will not be correctly orientated with respect to compass directions). In other words it has recreated the original data from which the distances were measured.
Non-metric multidimensional scaling (NMDS)
As with a PCO the aim is to transform between-case distances into a set of Euclidean distances. However, in a NMDS analysis the rank order of the original distances is assumed to contain the necessary information. The aim is to reproduce, as closely as possible, the rank order of the distances from the original distance matrix in the final Euclidean distance matrix which can then be projected, via an iterative algorithm, into lower dimensional space.
Example Analysis
This analysis uses Fisher's iris data set and is available as a text file. The analysis was completed using the excellent, and free PAST software. The iris data consist of four flower measurements from three species of Iris. In the many analyses of these data it is relatively easy to separate out the I. setosa flowers from those of the other two species. Two different distance measure were used (Gower's and Euclidean distance).
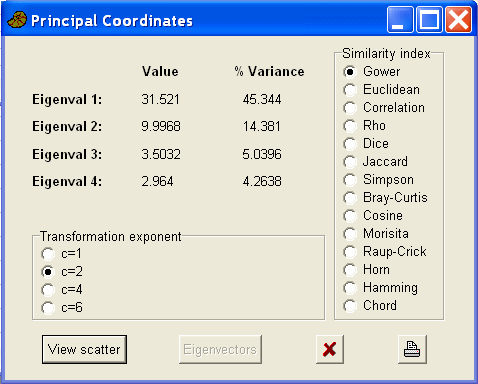
Gower's similarity measure
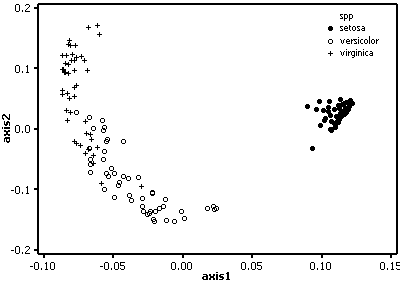
The setosa samples are well separated and form a tight cluster, while there is considerable overlap between the other two species.
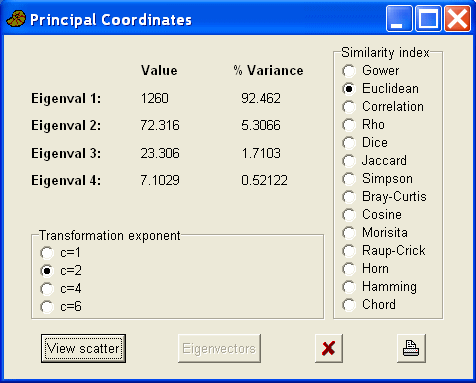
Euclidean distance measure
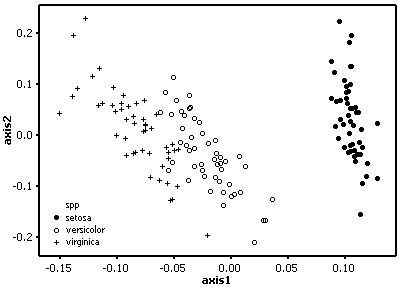
The setosa samples are again well separated but form a looser cluster. Although there is overlap between the other two species it is less than the results using Gower's measure.