Skip to main content

Analysis 4 Extracting 3 factors, Varimax rotation and Factor Loading graphs produced

Since one the main aims of these analyses is reducing the dimensionality of the data it makes little sense to work with 5 components rather than 5 variables, so how do we decide the number of factors to retain? Several methods have been suggested, of which the two most common are:

  1. Only retain those components/factors whose eigenvalue is >= 1.000, this would result in the retention of just the first two components.

  2. Examine a 'scree plot' of the eigen values against the number of factors. The appropriate number of factors is given if there is a break in slope. In this example, three components would seem to be needed.

By default Minitab extracts as many factors as there are variables. If you wish to have fewer factors extracted this must be specified in the "Number of factors to extract" box. In this example three are extracted because of the results from the scree plot.

Factor Analysis window showing 3 factors to be extracted and varimax rotation

Factor Analysis: V1, V2, V3, V4, V5

Principal Component Factor Analysis of the Correlation Matrix

Unrotated Factor Loadings and Communalities

Variable Factor1  Factor2  Factor3 Communality
V1      -0.803    0.337    0.342   0.876
V2      -0.947   -0.170   -0.164   0.952
V3      -0.919   -0.099   -0.274   0.929
V4      -0.192   -0.837    0.476   0.964
V5       0.159   -0.894   -0.255   0.889
Variance 2.4480   1.6518   0.5110  4.6108
% Var    0.490    0.330    0.102   0.922

Rotated Factor Loadings and Communalities

Varimax Rotation

Variable Factor1 Factor2 Factor3 Communality
V1       0.575   -0.733   0.091  0.876
V2       0.956   -0.113   0.160  0.952
V3       0.960   -0.076   0.032  0.929
V4       0.115    0.162   0.962  0.964
V5       0.062    0.812   0.475  0.889
Variance 2.1844   1.2406  1.1858 4.6108
% Var    0.437    0.248   0.237  0.922

Sorted Rotated Factor Loadings and Communalities

This is the important section. It shows that:

Variable Factor1  Factor2  Factor3  Communality
V3       0.960    0.000    0.000    0.929
V2       0.956    0.000    0.000    0.952
V5       0.000    0.812    0.475    0.889
V1       0.575   -0.733    0.000    0.876
V4       0.000    0.000    0.962    0.964
Variance 2.1844   1.2406   1.1858   4.6108
% Var    0.437    0.248    0.237    0.922

Factor Score Coefficients

Variable Factor1 Factor2  Factor3
V1       0.036  -0.697    0.333
V2       0.486   0.146   -0.075
V3       0.547   0.265   -0.249
V4      -0.196  -0.319    0.996
V5       0.190   0.711    0.068

This is the loading plot for Factors 1 and 2. Note that I have added the red axes

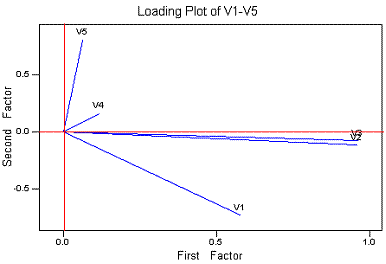
Loading plot v1-v5 against Factors 1 & 2

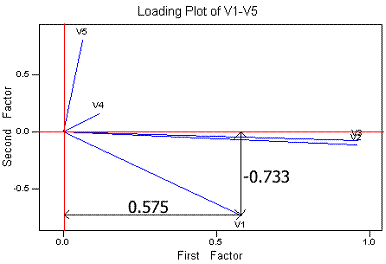
The lines are drawn to the coordinates for a variable that are the factor loadings. For example, V1 has rotated loadings of 0.575 on Factor 1 and -0.733 on Factor 2.

Loading plot v1-v5 against Factors 1 & 2. Demonstrates how the ends of the vectors are the factor loadings.

These plot are interpreted by looking for plots that close (parallel) to an axis and as long as possible. In the above this shows that Factor 1 (the horizontal axis) is mainly V2 and V3 while Factor 2 (vertical) is mainly V5. V1 contributes to both while V4 makes little contribution to either.

Back to PCA Example 1