Cluster Analysis SAQ notes

Calculating Binary Measures

One big disadvantage of Minitab is that, unlike SPSS, it does not provide Binary similarity measures. However, for a small number of cases it is feasible to do the calculations by hand.

The key to understanding Binary measures is the matrix of agreement. One of these must be calculated for each pair of cases and it has four numbers labelled a, b, c and d where:

a is the number of variables that have a 1 for both cases (i.e. is present in both)

b is the number of variables that have a 1 for case 1 only.

c is the number of variables that have a 1 for case 2 only.

b is the number of variables that have a 0 for both cases (i.e. absent from both).

You may also need n, the number of variables

For example, using the SAQ data file ( I have re-labelled the variables V1-V5 to avoid confusion with the matrix of agreement names a - d).

Case	V1	V2	V3	V4	V5
1	1	1	1	0	1
2	1	1	1	0	0
3	1	0	0	1	1
4	1	0	1	1	1
5	0	0	1	1	0

In the following examples I have labelled each variable with a, b, c or d as appropriate.

Case 1 v case 2.

Case	V1	V2	V3	V4	V5
1	1	1	1	0	1
2	1	1	1	0	0
	a	a	a	d	b

Therefore a = 3, b = 1, c = 0, d = 1 and n = 5

Case 2 v case 3

Case	V1	V2	V3	V4	V5
2	1	1	1	0	0
3	1	0	0	1	1
	a	b	b	c	c

Therefore a = 1, b = 2, c = 2, d = 0 and n = 5

Once you have the frequencies for a, b, c and d you substitute them into the appropriate formula for a distance measure.

The simple matching coefficient is (a + d)/n, therefore

For Case 1 v Case 2 the simple matching coefficient is (3 + 1)/5 = 5/5 = 0.8

For Case 2 v Case 3 the simple matching coefficient is (1 + 0)/5 = 1/5 = 0.2

The Dice coefficient is 2a/(2a + b + c), therefore

For Case 1 v Case 2 the Dice coefficient is 6/(6 + 1 + 0) = 6/7 = 0.857 (3dp)

For Case 2 v Case 3 the Dice coefficient is 2/(2 + 2 + 2) = 2/6 = 0.333 (3dp)

The Pattern Difference coefficient is bc/(n²), therefore

For Case 1 v Case 2 the Pattern Difference coefficient is 1 x 0 / 5² = 0/25 = 0

For Case 2 v Case 3 the Pattern Difference coefficient is 2 x 2 / 5² = 4/25 = 0.16

Calculating and viewing distance matrices in Minitab

Minitab can calculate, store and display distance matrices should you wish to see them although it is not something that I have ever found particularly informative. The most important part of a Cluster Analysis, and the only part that you need for interpretation is the Dendrogram.

However, should you wish to see the distance matrix this is what you need to do.

These explanations use the SAQ interval variable data. It is assumed that C1 is Case, C2 is x and C3 is y.

First select the analysis options. In this example the Linkae Method is "Complete" and the Distance Measure is "Euclidean". Finally, don't forget to tick the Show Dendrogram option to see the dendrogram!

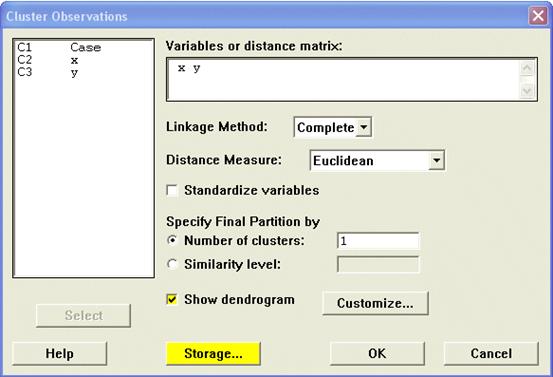
Minitab CLuster Observation Command Window

If you wish to store the distance matrix you must click the Storage button on the Cluster Observations command window. This opens up another window and you enter a matrix name into the appropriate place (labelled "Distance Matrix"). Note that matrices have names consisting of the letter M (or m) followed by a number, e.g. m1, M4, m101, etc. In the following example I have used the name M1.

Minitab Cluster Observation Storage options window

Now you need to find a way of displaying the distance matrix. The last command from the Data menu is "Display Data".

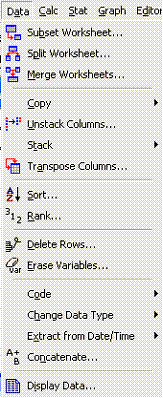
If you select this another window appears and you select M1 as the data you wish to display.

The output from this command appears in the Minitab Session window.

MTB > Print M1.

Data Display

Matrix M1

 0.000000 2.000000 6.403124 10.295630 9.219544 
 2.000000 0.000000 5.000000  8.602325 7.810250 
 6.403124 5.000000 0.000000  4.123106 2.828427 
10.295630 8.602325 4.123106  0.000000 2.236068 
 9.219544 7.810250 2.828427  2.236068 0.000000

MTB >

You can compare this to the results from the SAQ for Euclidean Distances

Case	1	2	3	4	5
1	0.0
2	2.0	0.0
3	6.4	5.0	0.0
4	10.3	8.6	4.1	0.0
5	9.2	7.8	2.8	2.2	0.0